9) Vertically opposite angles
10) Supplementary angles
11) Vertical angles
12) Linear pair angles
13 Supplementary
14.vertically
What theorems can be used to find the value of the variables?
9) The given angles, a and b are formed on the opposite side of the intersection of two lines.
Therefore, the relationship between angles a and b is; a and b are vertically opposite angles.
Vertical angles are angles formed by two lines when they cross, and they are located on opposite relative to each other
10) The given angles are located on the same line and together form a straight line, therefore, they are linear pair angles
Linear pair angles are supplementary, therefore;
The relationship between angles a and b is that they are supplementary angles.
11) Angles b and the 79° angle are vertically opposite angles
From vertical angles theorem, angles that are vertically opposite angles are always congruent.
Therefore;
‹b is congruent to the 79° angle, which gives;
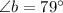
12) Angles b and the 49° angle are linear pair angles
linear pair angles are supplementary, therefore;
b + 49° = 180°
b = 180° - 49° = 121°
b = 121°
13) The 2•x angle and the 64° angle are supplementary angles, therefore;
2•x + 64° = 180°
2•x = 180° - 64° = 116°
x = 116°/2 = 58°
x = 58°
14) The (1 + 2•x)° and the 73° angles are vertically opposite angles, therefore;
(1 + 2•x)° = 73°
(2•x)° = (73 - 1)° = 72°
x = 72°/2 = 36°
x = 36°
15) (x + 2)° and 134° are linear pair angles, therefore;
(x + 2)° + 134° = 180°
(x + 2)° = 180° - 134° = 46°
x = 46° - 2° = 44°
x = 44°
16) 61° and (1 + 3•x)° are vertically opposite angles, therefore;
61° = (1 + 3•x)°
3•x° = (61 - 1)° = 62°
x = 62°/3 = 21°
x = 21°
17) The given angles are complementary angles, therefore;
6•x + 1 + 2•x + 1 = 8•x + 2 = 90°
8•x + 2 = 90°
8•x = 90° - 2
x = 88°
18) The given angles are complementary angles, therefore;
4•x + 3 + 35 = 90°
4•x = 90°- 38° = 52°
4•x
Therefore;
x = 52°/4 = 13°
x = 13°