Question

Select the graph of y = 3 sin (x - 1).

Answer 1

D.

Explanation:

The graph of 3 sin x will stretch vertically sin x by a factor 3. So 3 sin x will have a maximum value of 3 and a minimum of -3.

So it is either C or D.

The -1 in the parentheses will move the graph 1 unit to the right and as the graph of y = sin x passes through the origin, the required graph will pass through (1, 0) - so it is Graph D.

Answer 2

D.

Explanation:

We can cancel out choice A and choice B because both graphs' amplitude are 2. (Amplitude determines the max-min so if amplitude is 2 then max is 2 and min is -2)

Now for graph C and D, if we do not know how does sine graph shift, we will do substitution to find value of y when x = a.

Let's try x = 0 because both graphs have different y-value for x = 0.

`\displaystyle \large{y = 3 \sin(x - (\pi)/(4) ) } \\ \displaystyle \large{y = 3 \sin(0 - (\pi)/(4) ) } \\ \displaystyle \large{y = 3 \sin( - (\pi)/(4) ) }`

Let's recall the negative measure;-

`\displaystyle \large{ \sin( - x) = - \sin(x) }`

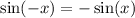
Therefore:-

`\displaystyle \large{y = - 3 \sin( (\pi)/(4) ) } \\ \displaystyle \large{y = - 3 \cdot \sin( (\pi)/(4) ) }`

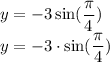
We know that π/4 is equivalent to 45° because π is defined as 180° and 180°/4 is 45°

Using hand method, sin(45°) is √2/2

`\ \displaystyle \large{y = - 3 \cdot ( √(2) )/(2) } \\ \ \displaystyle \large{y = ( - 3√(2) )/(2) }`

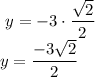
Looks like when we substitute x = 0, the y-value becomes negative.

The only graph that's reasonable is D.

Another method is you substitute x = π/4 in which would make y-value = 0.

Since π/4 is between 0 < x < π/2, the graph D is correct because graph C may have amplitude of 3 but y-value does not become 0 when substitute x = π/4

So D.