Question

Please factor and show work

Answer 1

`2a^2b*(3a^2-5ab-3b^2)`

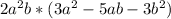
Explanation:

Attempt factorization by grouping

(((6•(a^4))•b)-((10•(a^3))•(b^2)))-((2•3a^2)•b^3)

(((6•(a^4))•b)-((2•5a^3)•b^2))-(2•3a^2b^3)

(((2•3a^4) • b) - (2•5a^3b^2)) - (2•3a^2b^3)

6a^4b - 10a^3b^2 - 6a^2b^3 = 2a^2b • (3a^2 - 5ab - 3b^2)

Pull out the leading term and put it with the original equation

= 2a^2b • (3a^2 - 5ab - 3b^2)

This would be one of the quicker ways to factor this equation.

Hope this helps.