Answer:
Explanation:
(a). 2( 2 )³ + a ( 2 )² - b ( 2 ) + 12 + ( 18 ) = 0
16 + 4a - 2b + 30 = 0
4a - 2b = - 46
2a - b = - 23 ....... ( 1 )
2 ( - 4 )³ + a ( - 4 )² - b ( - 4 ) + 12 = 0
- 128 + 16a + 4b + 12 = 0
16a + 4b = 116
4a + b = 29 ........ ( 2 )
( 1 ) + ( 2 )
6a = 6 , a = 1
4(1) + b = 29 , b = 25
(b). 2x³ + x² + 25x + 12 = 0
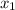 = - 4 ( given: f(x) is divisible by x + 4 )
= - 4 ( given: f(x) is divisible by x + 4 )
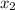 = 0.5
= 0.5
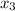 = 3
= 3