In the differential equation
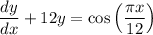
multiply on both sides by the integrating factor
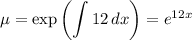
Then the left side condenses to the derivative of a product.

![(d)/(dx)\left[e^(12x)y\right] = e^(12x)\cos\left((\pi x)/(12)\right)](https://img.qammunity.org/2023/formulas/mathematics/college/bbwizn9zcymp1zr2rzlxkmxun8pa5yg48x.png)
Integrate both sides with respect to
 , and use the initial condition
, and use the initial condition
 to solve for the constant
to solve for the constant
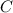 .
.
![\displaystyle \int (d)/(dx) \left[e^(12x)y\right] \, dx = \int e^(12x) \cos\left((\pi x)/(12)\right) \, dx](https://img.qammunity.org/2023/formulas/mathematics/college/zqr0lf6tt0ugpv31igoladlb5zew51bbv4.png)
As an alternative to integration by parts, recall
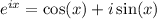
Now

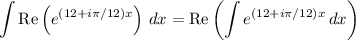
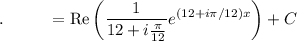
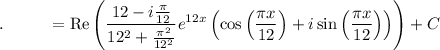
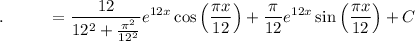

Solve for
 .
.
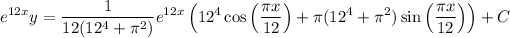
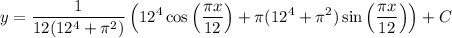
Solve for
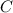 .
.
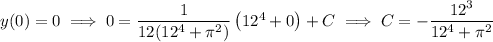
So, the particular solution to the initial value problem is

Recall that
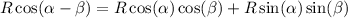
Let
 . Then
. Then
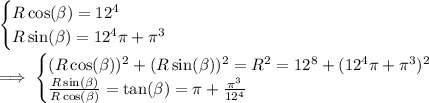
Whatever
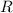 and
and
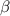 may actually be, the point here is that we can condense
may actually be, the point here is that we can condense
 into a single cosine expression, so choice (D) is correct, since
into a single cosine expression, so choice (D) is correct, since
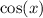 is periodic. This also means choice (C) is also correct, since
is periodic. This also means choice (C) is also correct, since
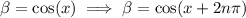 for infinitely many integers
for infinitely many integers
 . This simultaneously eliminates (A) and (B).
. This simultaneously eliminates (A) and (B).