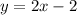Answer:
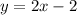
Explanation:
The x-intercept is when the line crosses the x-axis, so when y = 0.
Therefore, the two points on the line are:
To find the equation of the line when given two points from the line, first find the slope:

Now substitute the found slope and one of the points (1, 0) into the point-slope form of a linear equation:
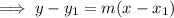
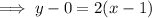
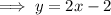
Therefore, the equation of the line is: