Question

If m<1 = (7x-19), and m<2 = (x + 5)°, find m2

Answer 1

Answer: m<2 = 18°

Explanation:
m<1 + m<2 = 90°

7x - 19 + x + 5 = 90°
First add common variables; 7x + x = 8x || -19 + 5 = -14
8x - 14 = 90°
Second add 14 on both sides;

8x - 14 = 90°

+14 +14

8x = 104°
Third divide 8 to 104

`(8x)/(8) = (104)/(8)`

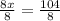
x = 13

m<1 7(13) - 19 + m<2 (13) + 5 = 90°
13 * 7 = 91
91 - 19 = 72
72 + 13 = 85
85 + 5 = 90°

m<2 = 13 + 5 = 18°

Hope this helps! :]
--Blu