Question

Solve the equation.

`\sqrt{y^(2)-20+100 } =y-10`

Answer 1

No solution.

Explanation:

So lets solve the square root.

Sqrt(y^2 - 20 + 100) = y - 10

Sqrt(y^2 + 80 = y - 10)

Solve time.

y^2 + 80 = y - 10 (We are squaring them)

y^2 + 80 = y^2 - 20y + 100

y^2 + 80 - y^2 = y^2 - 20y + 100 - y^2 (Subtract y^2 from both sides)

80 = -20y + 100

Flip it

-20y + 100 = 80

-20y + 100 - 100 = 80 - 100 (Subtract 100 from both sides)

-20y = -20

Now divide both sides by -20

-20y/-20 = -20/-20

y = 1

All you would do is plug in the values and you get...

`9 \\eq -9`

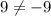
This is false.