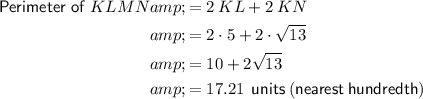Answer:
1. 18.81 units
2. 17.21 units
Explanation:
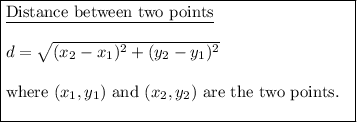
Question 1
Given vertices of ΔABC:
- A = (-2, 3)
- B = (3, -3)
- C = (-2, -3)
Plot the vertices on the given graph paper and join with line segments to create the triangle.
As points B and C share the same y-coordinate:
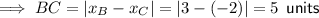
As points A and C share the same x-coordinate:
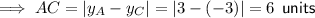
Use the distance formula to find the length AB:
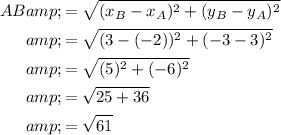
The perimeter of a two-dimensional shape is the distance all the way around the outside.
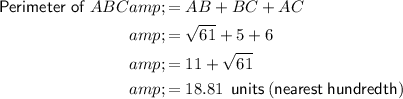
Question 2
Given vertices of polygon KLMN:
- K = (-1, 1)
- L = (4, 1)
- M = (2, -2)
- N = (-3, -2)
Plot the vertices on the given graph paper and join with line segments to create the polygon.
As the y-coordinate of points K and L, and M and N are the same, KL and MN are parallel line segments.
As the difference between the x-coordinates of K and N, and L and M is 2 units, KN and LM are parallel line segments.
Therefore, the polygon is a parallelogram.
A parallelogram has two pairs of opposite sides that are equal in length.
Therefore, KL = NM and KN = LM.
As points K and L share the same y-coordinate:
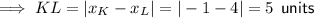
Use the distance formula to find the length KN:
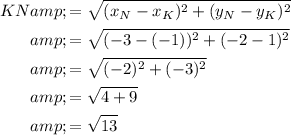
The perimeter of a two-dimensional shape is the distance all the way around the outside.