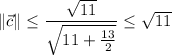Question

asked Jul 1, 2023 200k views

1 Answer

Kevin Yin · Answer 1 · 2023-07-06T14:21:50+0000

Computing the matrix product in the last condition gives a system of linear equations in the components of
$\vec c$ ,

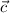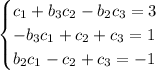
$\begin{cases} c_1 + b_3c_2 - b_2c_3 = 3 \\ -b_3c_1 + c_2 + c_3 = 1 \\ b_2c_1 - c_2 + c_3 = -1 \end{cases}$

and is easily solvable to get

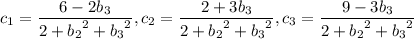
$c_1 = \frac{6-2b_3}{2+{b_2}^2+{b_3}^2}, c_2 = \frac{2+3b_3}{2+{b_2}^2+{b_3}^2}, c_3 = \frac{9-3b_3}{2+{b_2}^2+{b_3}^2}$

or, using the condition
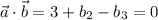$\vec a\cdot\vec b = 3 + b_2 - b_3 = 0$ ,

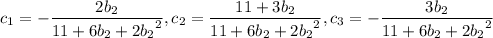
$c_1 = -\frac{2b_2}{11 + 6b_2 + 2{b_2}^2}, c_2 = \frac{11+3b_2}{11+6b_2+2{b_2}^2}, c_3 = -\frac{3b_2}{11+6b_2+2{b_2}^2}$

• (1) is false, since

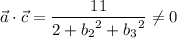
$\vec a \cdot \vec c = \frac{11}{2 + {b_2}^2 + {b_3}^2} \\eq 0$

because
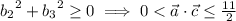${b_2}^2+{b_3}^2\ge0 \implies 0<\vec a\cdot\vec c\le\frac{11}2$ .

• (2) is true.

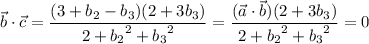
$\vec b\cdot \vec c = \frac{(3 + b_2 - b_3) (2 + 3b_3)}{2 + {b_2}^2 + {b_3}^2} = \frac{(\vec a\cdot\vec b)(2+3b_3)}{2+{b_2}^2+{b_3}^2} = 0$

• (3) is false. The magnitude of
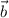$\vec b$ could be smaller than √10.

Since
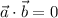$\vec a\cdot\vec b=0$ , we have

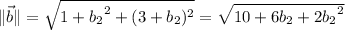
$\|\vec b\| = \sqrt{1 + {b_2}^2 + (3+b_2)^2} = \sqrt{10 + 6b_2 + 2{b_2}^2}$

and

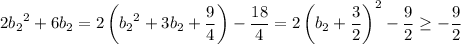
$2{b_2}^2 + 6b_2 = 2\left({b_2}^2 + 3b_2 + \frac94\right) - \frac{18}4 = 2\left(b_2 + \frac32\right)^2 - \frac92 \ge - \frac92$

which is to say,
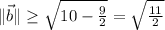$\|\vec b\| \ge √(10-\frac92) = \sqrt{\frac{11}2}$ .

• (4) is true.

We have

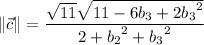
$\|\vec c\| = \frac{√(11) \sqrt{11 - 6b_3 + 2{b_3}^2}}{2 + {b_2}^2 + {b_3}^2}$

In terms of
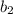b_2 alone,

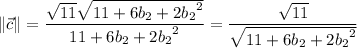
$\|\vec c\| = \frac{√(11)\sqrt{11 + 6b_2 + 2{b_2}^2}}{11+6b_2+2{b_2}^2} = \frac{√(11)}{\sqrt{11+6b_2+2{b_2}^2}}$

Now,

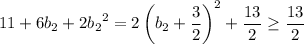
$11 + 6b_2 + 2{b_2}^2 = 2\left(b_2+\frac32\right)^2 + \frac{13}2 \ge \frac{13}2$

which means

$\|\vec c\| \le \frac{√(11)}{\sqrt{11 + \frac{13}2}} \le √(11)$

Please log in or register to add a comment.