In the polynomial $(ax^6 bx^8 cx^3 d)(x^5 ex^4 f)(x^2 gx h)$, letters $a$ through $h$ are all nonzero constants. what is the degree of the polynomial?

Question

asked Apr 21, 2023 164k views

1 Answer

Honeal · Answer 1 · 2023-04-25T23:04:49+0000

I assume you mean the polynomial

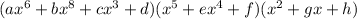
(ax^6 + bx^8 + cx^3 + d) (x^5 + ex^4 + f) (x^2 + gx + h)

The degree of this polynomial is the exponent of the largest power of
in the expansion of the product.

This term is the product of the largest power terms in each factor. These are

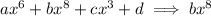
$ax^6 + bx^8 + cx^3 + d \implies bx^8$

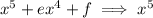
$x^5 + ex^4 + f \implies x^5$

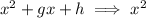
$x^2 + gx + h \implies x^2$

So, the largest power term in the polynomial is

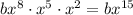
$bx^8 \cdot x^5 \cdot x^2 = bx^(15)$

and the degree is 15.