The angle made by the vector is
 such that
such that
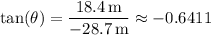
Before taking the inverse tangent of both sides, recall that
 returns a number between -π/2 and π/2 radians, or -90° and +90°. The vector in the diagram clearly makes an angle between 90° and 180°, however, so we use the fact that tangent has a period of π rad / 180° to write
returns a number between -π/2 and π/2 radians, or -90° and +90°. The vector in the diagram clearly makes an angle between 90° and 180°, however, so we use the fact that tangent has a period of π rad / 180° to write
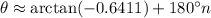
where
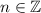 .
.
Now,
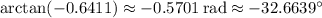
Add 180° to this to recover the correct angle.
