Answer:
Areas under the curve
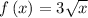 ,
,
![[1,4]](https://img.qammunity.org/2023/formulas/mathematics/college/k5the6i7zohp19k55ocyfehll77tzudapg.png) : 14
: 14
Explanation:
The area under a curve on an interval [a, b] is the integral of the function computed in this interval :

(1) For
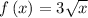 with
with
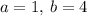
area
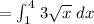 =
=
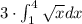 =
=
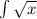 =
=
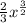
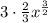 =
=
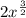
At
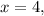 we get
we get
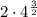 =
=
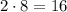
At
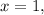 we get
we get
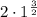 =
=
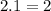
So area under the curve for
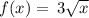 in the interval
in the interval
![[1, 4] = 14](https://img.qammunity.org/2023/formulas/mathematics/college/h6dzm8c2gc2rtkp523h7pwyb4roi1aig8b.png)
(2)
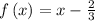
 =
=
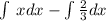
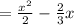
![\left[(x^2)/(2)\right]^(27)_1 = (27^2)/(2) - (1)/(2) = (729)/(2)-(1)/(2) = (728)/(2) = 364](https://img.qammunity.org/2023/formulas/mathematics/college/sa0aunokgzw2mvw8wr1ortaqdym5buf9re.png)
![\left[(2)/(3)x\right]^(27)_1 = (2)/(3)\cdot \:27 - (2)/(3)\cdot \:1 = 18-(2)/(3) = (52)/(3)](https://img.qammunity.org/2023/formulas/mathematics/college/gnbpeztdti4dqw91jzbzzj2w6kg0o0p5zs.png)
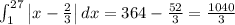 (Answer)
(Answer)