Answer:
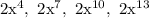
===========================================================
Step-by-step explanation:
The first term is
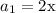 and the common ratio is
and the common ratio is

To get the second term, we multiply the first term by that common ratio
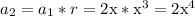
Repeat a similar idea for the third term

and the fourth term is
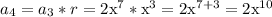
The fifth term is
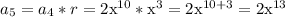
Something to notice: The exponents of the first five terms are: 1, 4, 7, 10, 13. The sequence of exponents is arithmetic even though the original underlying sequence is geometric.
The reason why the exponent sequence is arithmetic is because we keep multiplying by
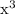 , and hence we keep adding 3 to each exponent to get the next exponent.
, and hence we keep adding 3 to each exponent to get the next exponent.
-----------------------------------------
To summarize, the first five terms are:
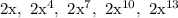
We will ignore the first term 2x since your teacher wanted you to find the next four terms after that first term (i.e. term2 through term5).