Question

Pls help w this pretty urgent

Answer 1

`\begin{aligned} \textsf{a)} \quad & \textsf{Position function}: \quad s(t) = -16t^2+1362 \\ & \textsf{Velocity function}: \quad v(t) = -32t\end{aligned}`

`\textsf{b)} \quad \overline{v}=-48\:\: \sf ft/s`

`\begin{aligned}\textsf{c)} \quad v(1) & = -32\:\: \sf ft/s\\ v(2) & = -64\:\: \sf ft/s\end{aligned}`

`\textsf{d)} \quad t = 9.226\:\: \sf s \:\: (3\: d.p.)`

`\textsf{e)} \quad v = -292.242\:\: \sf ft/s \:\: (3\: d.p.)`

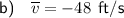
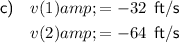
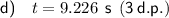
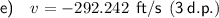
Explanation:

Given:

`s(t)=-16t^2+v_0t+s_0`

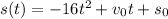
Part (a)

If v₀ is the initial velocity, and s₀ is the initial position:

`\implies v_0=0`

`\implies s_0=1362`

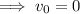
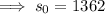
Therefore:

`\begin{aligned}\textsf{Position function}: \quad s(t) & =-16t^2+0+1362\\ \implies s(t) & = -16t^2+1362 \end{aligned}`

`\begin{aligned}\textsf{Velocity function}: \quad v(t)&=s\:'(t)\\ \implies v(t) &=-32t\end{aligned}`

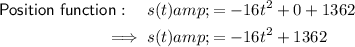
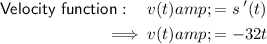
Part (b)

Average velocity is the change in displacement divided by the change in time:

`\overline{v}=(s(t_2)-s(t_1))/(t_2-t_1)`

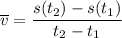
Given interval: 1 ≤ t ≤ 2

`\implies t_1=1`

`\implies t_2=2`

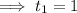
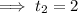
Find the values of s(t) at t = 1 and t = 2:

`\implies s(1)=-16(1)^2+1362=1346`

`\implies s(2)=-16(2)^2+1362=1298`

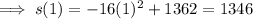
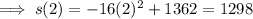
Substitute the values into the formula:

`\overline{v}=(s(2)-s(1))/(2-1)=(1298-1346)/(2-1)=-48\:\: \sf ft/s`

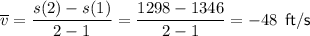
Part (c)

To find the velocity at t = 1 and t = 2, substitute these values into the velocity function found in part (a):

`\implies v(1)=-32(1)=-32\:\: \sf ft/s`

`\implies v(2)=-32(2)=-64\:\: \sf ft/s`

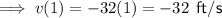
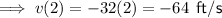
Part (d)

The time required for the coin to reach ground level is when s(t) = 0:

`\begin{aligned}s(t) & = 0\\-16t^2+1362 & = 0\\16t^2 & = 1362\\t^2 & = 85.125\\t & = √(85.125)\\t & = 9.226\: \sf s\:\:(3\:d.p.)\end{aligned}`

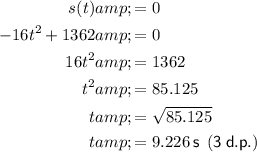
Part (e)

To find the velocity of the coin at impact with the ground, substitute the found value of t from part (d) into the equation for velocity found in part (a):

`\begin{aligned}v(t) & = -32t\\\implies v(√(85.125)) & = -32(√(85.125))\\ v & =-295.242\:\: \sf ft/s\:\:(3\:d.p.)\end{aligned}`

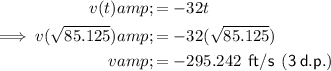
Note: I have used the non-rounded value of t from part (d) for accuracy.