Question

What is an equation of the line that passes through the point (8,-2) and is perpendicular to the line 4x+3y=3

Answer 1

`y = (3)/(4)x - 8`

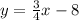
Explanation:

We know that the slope of a line perpendicular to a line with a given slope is the negative reciprocal of that given slope. We are given that we want a line perpendicular to that of 4x + 3y = 3. To find the slope of this given line, we put it into slope intercept form y = mx + b where m is the slope:

`4x + 3y = 3`

`3y = 3 - 4x`

`y = 1 - (4)/(3)x`

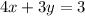
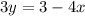
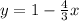
So we have that the slope of our given line is -4/3. The negative reciprocal of this is 3/4. We thus have that the slope of the line we are looking for is 3/4.

We then know that the equation of the line we want fits the form
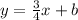`y=(3)/(4) x + b`, which we know through point slope form. We are then given that (8, -2) is a point on this line. Plugging in:

`-2 = (3)/(4)(8) + b`

`-2 = 6 + b`

`b = -8`

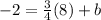
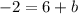
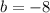
We then get the equation of the line we are looking for as
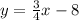`y = (3)/(4)x - 8`.