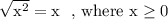Answer: Choice B) 9/10
===================================================
Work Shown:
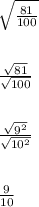
Therefore,
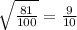
--------------------
Explanation:
I broke up the single square root to make a fraction of square roots. Then I rewrote 81 as 9^2, and 100 as 10^2. This is so the square roots cancel out with the squares.
The general rule is that