Exact Distance =
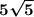 units
units
Approximate Distance = 11.1803 units
===================================================
Work Shown:
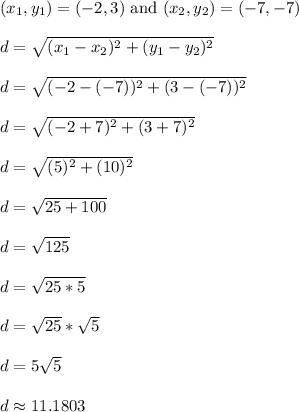
The exact distance is
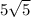 units, which approximates to about 11.1803 units
units, which approximates to about 11.1803 units
I used the distance formula. Round the approximate value however your teacher instructs.
A slight alternative is to plot the two points to form a right triangle. The hypotenuse goes from (-2,3) to (-7,-7). Then use the pythagorean theorem.
You can use tools like WolframAlpha or GeoGebra to confirm the answer.