Question

The length of a rectangle is 4 inches greater than twice the width. If the diagonal is 2 inches more than the length, find the dimensions of the rectangle.

Answer 1

The dimensions are 10 inches and 24 inches.

Explanation:

Since the quadrilateral is a rectangle, the diagonal divides the rectangle into two right triangles. That means we can use the Pythagorean Theorem, which applies only to right triangles.

On the bottom left triangle, the sides forming the right angle are the legs. They measure x and 2x + 4. The are a and b in the Pythagorean Theorem equation. The side of the triangle measuring 2x + 6 is the hypotenuse of the right triangle, the side opposite the right angle and the longest side in a right triangle. The hypotenuse is c in the Pythagorean Theorem equation.

Start with the equation of the Pythagorean theorem.

`a^2 + b^2 = c^2`

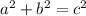
Now substitute the values we have for a, b, and c.

`(x)^2 + (2x + 4)^2 = (2x + 6)^2`

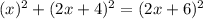
Square the two binomials. You an use the pattern:

`(a + b)^2 = a^2 + 2ab + b^2`

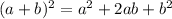
which I will use, or you can use FOIL and collect like terms.

`x^2 + 4x^2 + 16x + 16 = 4x^2 + 24x + 36`

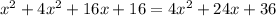
Collect like terms, and move all terms to the left side equaling zero.

`5x^2 + 16x + 16 = 4x^2 + 24x + 36`

`x^2 - 8x - 20 = 0`

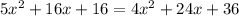
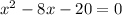
Try to factor the left side. We need two numbers whose product is -20 and whose sum is -8. -10 and 2 work.

`(x - 10)(x + 2) = 0`

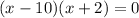
Set each factor equal to zero, and solve for x.

x - 10 = 0 or x + 2 = 0

x = 10 or x = -2

Since one side of the rectangle measures x, x = -2 cannot be a solution since you cannot have a negative side length.

x = 10 is acceptable.

2x + 4 = 2(10) + 4 = 24

Answer: The dimensions are 10 inches and 24 inches.