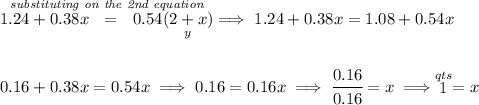Question

7) Krystal wants to make a 54% sugar

solution. She has already poured 2 qt. of a
62% sugar solution into a beaker. How
many qt. of a 38% sugar solution must she
add to this to create the desired mixture?

Answer 1

we know she poured already 2 qts of a 62% sugar solution, hmmm how much will that be in quarts? well, just (62/100) * 2 = 1.24 quarts.

we also know she wants to mixed say "x" quarts of a 38% sugar solution, how many quarts will that be? well, (38/100) * x = 0.38x.

let's make a quick table from that as well as including the desired mixture.

`\stackrel{\textit{substituting on the 2nd equation}}{1.24 + 0.38x ~~ = ~~ 0.54(\underset{y}{2 + x})}\implies 1.24+0.38x=1.08+0.54x \\\\\\ 0.16+0.38x=0.54x\implies 0.16=0.16x\implies \cfrac{0.16}{0.16}=x\implies \stackrel{qts}{1}=x`