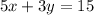Answer:
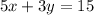
Explanation:
The x-intercept is 3, so the ordered pair of that point is (3, 0).
The y-intercept is 5, so the ordered pair of that point is (0, 5).
We need the equation of the line that passes through points (3, 0) and (0, 5). Also, from the y-intercept, we know that b = 5 in the slope-intercept form of the equation of a line,
y = mx + b
b = 5
We now have:
y = mx + 5
We can find the slope using the two given points.

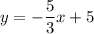
Now we change the equation into standard form,
ax + by = c
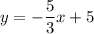
Multiply both sides by 3.
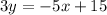
Rearrange terms.