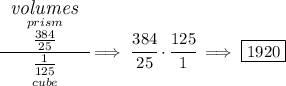Question

How many cubes with edge length 1/5 inch fit in a prism that measures 2 2/5 inches by 3 1/5 inches by 2 inches?​

Answer 1

first off, let's change the mixed fractions to improper fractions and let's check what the volume in in³ for the prism is.

`\stackrel{mixed}{2(2)/(5)}\implies \cfrac{2\cdot 5+2}{5}\implies \stackrel{improper}{\cfrac{12}{5}} ~\hfill \stackrel{mixed}{3(1)/(5)}\implies \cfrac{3\cdot 5+1}{5}\implies \stackrel{improper}{\cfrac{16}{5}} \\\\\\ \stackrel{\textit{volume of the prism}}{ \cfrac{12}{5}\cdot \cfrac{16}{5}\cdot 2\implies \cfrac{384}{25}}~in^3`

now, we know the small cubes have an "edge" or namely a side of 1/5, let's get their volume as well
`\cfrac{1}{5}\cdot \cfrac{1}{5}\cdot \cfrac{1}{5}\implies \cfrac{1}{125}~in^3`

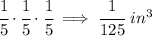
now, how many times does the volume of one small cube, go into the volume of the containing prism?

`\stackrel{\textit{\large volumes}}{\cfrac{~~~~ \stackrel{prism}{(384)/(25)}~~~~}{\underset{cube}{(1)/(125)}}}\implies \cfrac{384}{25}\cdot \cfrac{125}{1}\implies \boxed{1920}`