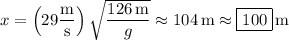The car's vertical position
 at time
at time
 is
is
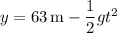
since it starts 63 m above the ground, and after leaving the cliff it accelerates downward due to gravity.
Its horizontal position
 is
is
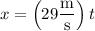
since the car leaves the cliff horizontally at 29 m/s, and is not influenced by any other acceleration in this plane.
1. Solve for
 such that
such that
 .
.
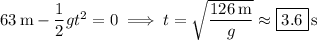
2. Solve for
 at this value of
at this value of
 .
.