Question

Find the zeros of the function. Enter the solutions from least to greatest.

f(x) = (x + 2)^2 - 16

Answer 1

x = 2, x = -6

Explanation:

Given quadratic function in vertex form:

`f(x)=(x+2)^2-16`

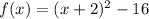
The zeros of a function occur when f(x) = 0:

`\implies (x + 2)^2 - 16 = 0`

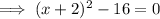
Add 16 to both sides:

`\implies (x + 2)^2 - 16+16 = 0+16`

`\implies (x + 2)^2 =16`

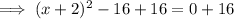
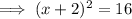
Square root both sides:

`\implies √( (x + 2)^2) =√(16)`

`\implies x+2= \pm 4`

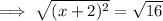
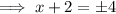
Subtract 2 from both sides:

`\implies x+2-2= -2 \pm 4`

`\implies x= -2 \pm 4`

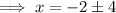
Therefore:

`\implies x=-2+4=2`

`\implies x=-2-4=-6`

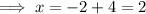
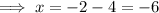
The zeros of the given quadratic function are x = 2, x = -6.