Question

The 6th term of a GP is -2 and its first term is 18 . what is the common ratio

Answer 1

Given conditions:

6th term (T6) = -2

first term (a) = 18

n = 6, r = ?

Formula for finding the nth term of a GP:

`tn = a {r}^(n - 1)`

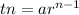
Where:

T = the given value for the number of term(s)

n = the given number of term

a = The first term

r = The common ratio

Replacing for the values:

`- 2 = 18 {r}^(6 - 1) \\ - 2 = 18 {r}^(5)`

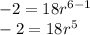
Dividing both sides by 18, we have:

`{r}^(5) = ( - 2)/(18)`

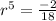
Now, we have to fifth root both sides to find the value of r.

`\sqrt[5]{ {r}^(5) } = \sqrt[5]{ ( - 2)/(18) }`

Therefore:

Common ratio,
`r = -0.0638165752`
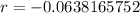
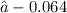`≈ -0.064` to 3 decimal places.

I hope this helps