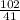Answer:
x =
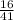
y =
Explanation:
To use elimination I need either the x terms to be inverses of each other or the y terms to be inverses of each other. There are a number of ways to do this. I am going to focus on the y's. If I multiple the first equation through by 5 and the second equation through by 3. I will make equivalent equations that will allow the y terms to be eliminated.
14x - 3y = -2
5(14x - 3y) =5(-2)
70x - 15y = -10
4x + 5y = 14
3(4x + 5y) = 3(14)
12x +15y =42
Add together the 2 bold equations above
70x - 15y = -10
12x + 15y = 42
82x = 32 Divide both sides by 82
x =
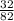 =
=
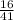
Plug this in either equation to solve for y
y =