Answer: No, the sides do not form a right triangle.
============================================================
Step-by-step explanation:
Let c = 20 be the largest or longest side. If we had a right triangle, then this side is the hypotenuse.
a = 14 and b = 15 are the other sides in either order.
Plug the values into the pythagorean theorem equation. Evaluate each side separately until getting a single numeric value.
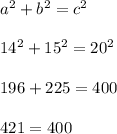
The last equation is false, so the first equation is false for those a,b,c values mentioned. This shows us we do not have a right triangle.
For more information, check out the pythagorean theorem converse.