Answer:
First term: 0.5
Sum of the first give terms: 30.5
Explanation:
General form of a geometric sequence:

where:
 is the nth term
is the nth term- a is the first term
- r is the common ratio
Given terms:
To find the common ratio r, divide consecutive terms:
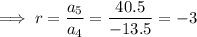
To find the first term, substitute the found value of r and one of the terms into the general formula:
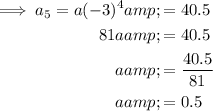
Sum of the first n terms of a geometric series:
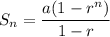
To find the sum of the first 5 terms of the geometric sequence, substitute n = 5 and the found values of a and r into the formula:
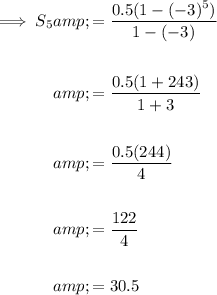
Therefore, the sum of the first 5 terms is 30.5.