Question

A shopkeeper packed two bags of sugar each 120 Kg into 3 Kg and 2 Kg packets respectively. There were half as many 2 Kg packets as 3 Kg packets. How many 3 Kg packets did he obtain?​

Answer 1

60

Explanation:

Since both bags of sugar were 120 kg, there is a total of 240 kg of sugar to be distributed into the packs. Let x represent the number of 2 kg packets and y represent the number of 3 kg packets. We know that all the sugar was packed into these two kinds of packets, so:

`2x+3y=240`

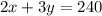
And we know that there were half as many 2 kg packets as 3 kg packets, so:

`x=(1)/(2) y`

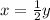
Now, we have a system of equations!

`\left \{ {{2x+3y=240} \atop {x=(1)/(2)y }} \right.`

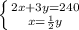
Let's put the second equation equal to y, since that removes the fraction:

`x=(1)/(2)y\\ 2x=y`

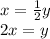
Now substitute y into the first equation:

`2x+3y=240\\2x+3(2x)=240`

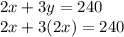
Now simplify to find x:

`2x+3(2x)=240\\2x+6x=240\\8x=240\\x=30\\`

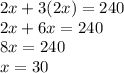
There are 30 of the 2 kg packets! Now, we can use x to find y, the number of 3 kg packets!

`2x=y\\2(30)=y\\60=y`

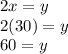
There are 60 of the 3 kg packets!