Question

Which ratios have a unit rate greater than 1? Choose ALL that apply.

9
8
9/5
5
-
miles: hour
6
miles: 3 hours
4)
1
4 miles: 3 hours
3
7 miles:
34
hour
121-1/4
2 miles : 3 hours
1
3
318
mile: 2 hours

Answer 1

A and E (top left and bottom middle)

Explanation:

Unit rates are found when a ratio has a denominator of 1. For the sake of simplicity, I will give the options in the image letter designations. A, B, and C are the top three from left to right, and D, E, and F are the bottom 3 from left to right.

A

`(9)/(5) miles:(5)/(6)hour`
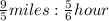
Because ratios can be written as fractions, this ratio can be written:

`((9)/(5))/((5)/(6))`
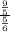
That's a mess! Another way to divide fractions is to multiply by the reciprocal of the denominator:

`(9)/(5)*(6)/(5)`

Since none of the terms can be cross-cancelled, multiply!

`=(54)/(25)`
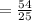
Since the numerator is greater than the denominator, the unit rate is greater than one!

B

`4miles:3(1)/(3)hours`

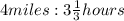
Start by turning the mixed number into an improper fraction:

`3(1)/(3)=(10)/(3)`

Now compare by multiplying 4 over 1 by the reciprocal of 10 thirds:

`(4)/(1)*(3)/(10)`

Cross-cancel and multiply:

`=(2)/(5)`

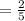
Since the numerator is less than the denominator, the unit rate is less than one!

C

`2(1)/(2) miles:3hours`
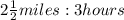
Convert the mixed number into an improper fraction:

`2(1)/(2) =(5)/(2)`
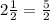
Multiply by the reciprocal of 3:

`(5)/(2)*(1)/(3)`
Multiply!

`(5)/(6)`
Since the numerator is less than the denominator, the unit rate is less than one!

D

`(9)/(5) miles :3hours`

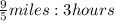
Multiply by the reciprocal of 3:

`(9)/(5)*(1)/(3)`

Cross cancel and multiply!

`=(3)/(5)`

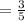
Since the numerator is less than the denominator, the unit rate is less than one!

E

`7 miles :(3)/(4)hour`

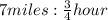
Multiply by the reciprocal of 3 fourths:

`(7)/(1)*(4)/(3)`

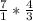
Multiply:

`=(28)/(3)`

Since the numerator is greater than the denominator, the unit rate is greater than one!

F

`(1)/(3)mile:2(3)/(8)hours`

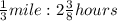
Convert the mixed number into an improper fraction:

`2(3)/(8)=(19)/(8)`

Multiply one third by the reciprocal of 19 eighths:

`(1)/(3)*(8)/(19)`
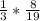
Multiply!

`=(8)/(57)`

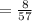
Since the numerator is less than the denominator, the unit rate is less than one!