Question

←

Save
Uranium-238 (U-238) has a half-life of 4.5 billion years. Geologists find a rock containing a mixture of U-238 and lead, and determine that 71% of the original U-238
remains; the other 29% has decayed into lead. How old is the rock?
The rock is ___ billion years old.
(Round to three decimal places as needed.)

Answer 1

Answer: 2.223 billion years old

Explanation:

since 71 percent of the rock is remaining, the half life hasn't been reached yet. Hence, we know uranium isn't 4.5 billion years old yet. However, every-time 4.5 billions years pass, the rock get smaller by 2 times(a scale factor of 1/2). Hence, you can express that in a log equation:

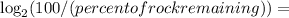`\log_(2)(100/(percent of rock remaining))=` Fraction of 4.5 billions years of time passed

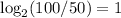`\log_(2)(100/50)=1` ==> 100% of 4.5 billion years passed. When 50% of rock remains, 4.5 billion years have passed.

`\log_(2)(100/100)` =

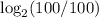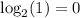`\log_(2)(1)=0` ==> 0% of 4.5 billion years passed. When the rock hasn't decayed at all yet, that means that it is 0 years old.

`\log_(2)(100/71)=0.494` ==> 49.4 % of 4.5 billion years passed

0.494*4.5 billion =2.223 billion years passed

2.223 billion years old