A. Find the number of sides of a polygon, The sum of whose interior angle is:
1. 1260°
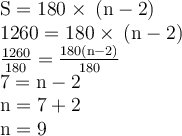
2. 1620°
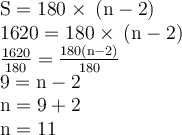
3. 1980°
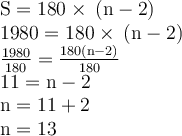
4. 4320°
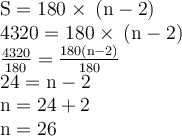
5. 1440°
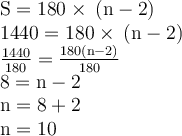
B. Calculate the sun of all the interior angle of a polygon having:
6. 5 sides
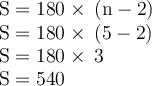
7. 7 sides
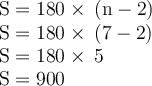
8. 9 sides
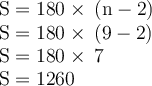
9. 10 sides
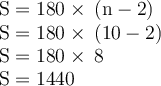
10. 11 sides
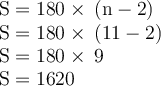
If there's a Latex Error, Please click the images attached below :)
Goodluck! :D