Question

Find the (perpendicular) distance from the line given by the parametric equations

x(t)= -2-6t
y(t)= 1-3t
z(t)= -5+7t
to the point (-8,9,8)

Answer 1

`\sqrt{(-(806)/(94)+8)^2+(-(215)/(94)-9)^2+ (-(251)/(94)-8)^2}` Whatever this number may be

Explanation:

The distance will be on the plane containing the point, and perpendicular to the line - which exists as long as the point doesn't sit on the line, but in that case our distance will simply be zero. Good news, since the line is given in parametric equation, the equation of the plane is easy to write by simply computing the dot product between the vector generating the line - or any multiple of it! - and the vector joining a random point x y z of the space with our given point, and setting it equal to zero. The equation of our plane is thus

`6(x-(-8)) + 3(y-9) -7(z-8) = 0\\6(x+8)+3(y-9)-7(z-8)=0`

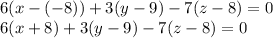
We could multiply now or later, doesn't matter, so let's wait. Now, we need to know when the line passes through the plane, so let's plug the (parametric) coordinate of the line and let's see for which value of t that happens:

`6(-2-6t+8) +3(1-3t -9) -7(-5+7t-8) =0\\6(6-6t) -3(8+3t)+7(13-7t)=0\\36-36t-24-9t+91-49t = 0\\t=103/94`

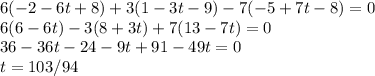
Found this value of t, we can use it to find the coordinate of the point in common between the line and the plane:

`(-2-6\frac {103}{94};1-3\frac {103}{94}; -5+7\frac {103}{94}) = (-(806)/(94);-(215)/(94);-(251)/(94))`

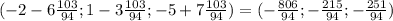
At this point it's simply a matter of calculating the distance between two points in 3D space, given by the usual
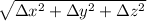`√(\Delta x^2+\Delta y^2+\Delta z^2)`, whatever abomination of a number it might become:

`\sqrt{(-(806)/(94)+8)^2+(-(215)/(94)-9)^2+ (-(251)/(94)-8)^2}`

At this point is a simple exercise in number crunching which I refuse to entertain more - but please double check all calculation above in case I didn't notice something.