Question

Help please!!!!!!!!!

Answer 1

(a) 3.5

(b) x = 4

(c) -¹/₂

(d) -¹/₂

Explanation:

Part (a)

f(1) is the value of y when x = 1.

To find the value of y from a given value of x, find the position of x on the x-axis, then trace vertically until you meet the line. Once you meet the line, trace horizontally to the y-axis to find the corresponding value of y.

Therefore, f(1) = 3.5.

Part (b)

To solve f(x) = 2, find the value of x when y = 2.

To find the value of x from a given value of y, find the position of y on the y-axis, then trace horizontally until you meet the line. Once you meet the line, trace vertically to the x-axis to find the corresponding value of x.

Therefore, the solution of f(x) = 2 is x = 4.

Part (c)

The average rate of change of function f(x) over the interval a ≤ x ≤ b is given by:

`(f(b)-f(a))/(b-a)`

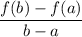
Given interval: 2 ≤ x ≤ 4

Therefore:

• a = 2
• b = 4

`\implies (f(4)-f(2))/(4-2)=(2-3)/(4-2)=-(1)/(2)`

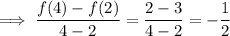
Part (d)

The average rate of change between any interval of the given function will be the same as the graph is linear. Therefore, the average rate of change from 0 to 8 is the same as the rate found in part (c): -¹/₂.

Proof

The average rate of change of function f(x) over the interval a ≤ x ≤ b is given by:

`(f(b)-f(a))/(b-a)`

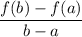
Given interval: 0 ≤ x ≤ 8

Therefore:

• a = 0
• b = 8

`\implies (f(8)-f(0))/(8-0)=(0-4)/(8-0)=-(4)/(8)=-(1)/(2)`