Answer:
127
Explanation:
Hey there! :)
Let us find the 18th term — first, there are two main types of sequences.
- Arithmetic Sequence — a sequence that has same difference or common difference.
- Geometric Sequence — a sequence that has same ratio.
But if you notice, it cannot be geometric sequence because if we do ratio test, there are no common ratios.
Hence, it can only be arithmetic sequence.
Common Difference
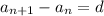
d is our common difference.
a_n+1 is the next term of a_n.
Let's check the common difference!
15-8 = 7
22-15 = 7
29-22 = 7
Therefore, 7 is our common difference.
General Terms of Arithmetic Sequence

We know that a1 is the first term of sequence which is 8.
Our common difference is 7.
We want to find the 18th term — therefore,

Therefore, the 18th term is 127.