Question

A cannonball is shot horizontally off a 10.5 m high castle wall at 47.4 m/s. How far from the base of the wall does the cannonball land?

Answer 1

69.8 m (nearest tenth)

Step-by-step explanation:

Constant Acceleration Equations (SUVAT)

`\boxed{\begin{array}{c}\begin{aligned}v&=u+at\\\\s&=ut+(1)/(2)at^2\\\\ s&=\left((u+v)/(2)\right)t\\\\v^2&=u^2+2as\\\\s&=vt-(1)/(2)at^2\end{aligned}\end{array}} \quad \boxed{\begin{minipage}{4.6 cm}$s$ = displacement in m\\\\$u$ = initial velocity in ms$^(-1)$\\\\$v$ = final velocity in ms$^(-1)$\\\\$a$ = acceleration in ms$^(-2)$\\\\$t$ = time in s (seconds)\end{minipage}}`

When using SUVAT, assume the object is modeled as a particle and that acceleration is constant.

Consider the horizontal and vertical motion of the projectile separately.

Resolving vertically

As the projectile is fired horizontally, the vertical component of its initial velocity is zero.

Acceleration due to gravity = 9.8 ms⁻²

Resolving vertically, taking ↓ as positive:

`s=10.5 \quad u=0 \quad a=9.8`

`\begin{aligned}\textsf{Using} \quad s&=ut+(1)/(2)at^2:\\\\10.5&=(0)t+(1)/(2)(9.8)t^2\\10.5&=4.9t^2\\t^2&=(15)/(7)\\t&=\sqrt{(15)/(7)}\end{aligned}`

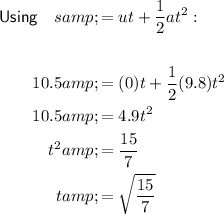
Resolving horizontally

The horizontal component of velocity is constant, as there is no acceleration horizontally.

Resolving horizontally, using the value of t found previously:

`u=47.7 \quad v=47.7 \quad a=0 \quad t=\sqrt{(15)/(7)}`

`\begin{aligned}\textsf{Using} \quad s&=ut+(1)/(2)at^2:\\\\s&=47.7\left(\sqrt{(15)/(7)}\right)+(1)/(2)(0)\left(\sqrt{(15)/(7)}\right)^2\\s&=47.7\left(\sqrt{(15)/(7)}\right)\\s&=69.82565022...\end{aligned}`

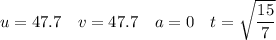
Therefore, the cannonball lands 69.8 m from the base of the wall.