Question

(x-4) |x-4| i am looking for the simplification of this. i think the answer should be x^2 - 16, my teacher gave us an answer, but i don't believe it is correct. she gave us -x^2 +8x - 16.

Answer 1

It depends on the sign of
`x-4`.

Recall the absolute value function's definition:

`|x| = \begin{cases}x & \text{if } x \ge 0 \\ -x & \text{if } x < 0\end{cases}`

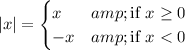
Now, if
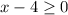`x-4\ge0`, then

`(x-4)|x-4| = (x-4)(x-4) = x^2 - 8x + 16`

On the other hand, if
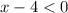`x-4<0`, then

`(x-4)|x-4| = -(x-4)(x-4) = -(x-4)^2 = -x^2 + 8x - 16`

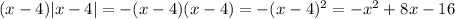
What you first suggested is incorrect. We have

`x^2 - 16 = (x - 4) (x + 4)`

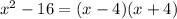
but
`|x-4| \\eq x + 4`.

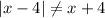We can show this using the definition again. If
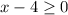`x-4\ge0`, then

`x-4 = x+4 \implies -4=4`

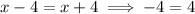
which is a contradiction; on the other hand, if
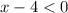`x-4<0`, then

`-x+4 = x+4 \implies 2x = 0 \implies x =0`

holds for only one value of
`x`.