In some base
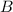 , we have
, we have
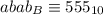
so that
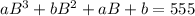
Factorize the left side.

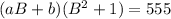
Now,
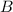 is a positive integer greater than 1, and
is a positive integer greater than 1, and
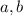 are positive integers taken from
are positive integers taken from
 . So consider the prime factorization of 555 on the right side.
. So consider the prime factorization of 555 on the right side.
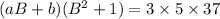
which we can write as
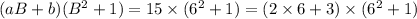
and so the base is 6, and the number in question is 2323₆.