Question

If $10^{51} - 9$ is written as an integer in standard form, what is the sum of the integer's digits?

Answer 1

Notice the pattern:

10² = 100, so 10² - 9 = 91 with a digital sum of 9 + 1 = 10

10³ = 1000, so 10³ - 9 = 991 with a digital sum of 2•9 + 1 = 19

10⁴ = 10000, so 10⁴ - 9 = 9991 with a digital sum of 3•9 + 1 = 28

Then for an arbitrary power of 10, we have

`10^n = 1\underbrace{00\ldots000}_(n\,\rm 0s) \implies 10^n - 1 = \underbrace{999\ldots99}_(n-1\,\rm9s)1 \\\\ \implies \text{digital sum} = 9(n-1)+1 = 9n - 8`

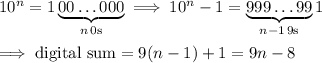
When
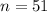`n=51`, the digital sum is 9•51 - 8 = 451.