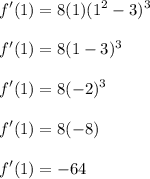Question

If f (x) = (x^2 − 3)^4, then f '(1) =

Answer 1

f'(1) = -64

Explanation:

To find f'(1), we will be finding the f'(x) first which means the first derivative of f(x), we can find the derivative by using chain rule to this function.

The formula of chain rule is:

`\displaystyle f(u) = u^n \to f'(u) = nu^(n-1)\cdot u'`

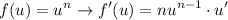
In simple explanation, we derive normally (power rule) then multiply by the derivative of inside (u).

Applying the formula, we will have:

`\displaystyle{f'(x)=4(x^2-3)^(4-1)\cdot (x^2-3)'}\\\\\displaystyle{f'(x)=4(x^2-3)^(3)\cdot 2x}\\\\\displaystyle{f'(x)=8x(x^2-3)^(3)}`

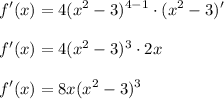
Substitute x = 1 in the f'(x):

`\displaystyle{f'(1)=8(1)(1^2-3)^3}\\\\\displaystyle{f'(1)=8(1-3)^3}\\\\\displaystyle{f'(1)=8(-2)^3}\\\\\displaystyle{f'(1)=8(-8)}\\\\\displaystyle{f'(1)=-64}`