Rewrite the function as
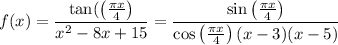
Vertical asymptotes occur wherever the denominator is zero (but not necessarily when the numerator is also zero).
We have
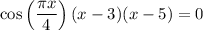
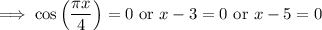
In the first case, we have
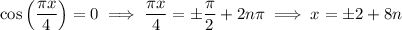
where
 is an integer. That is, any of
is an integer. That is, any of
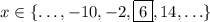 and
and
 are asymptotes.
are asymptotes.
In the latter two cases, we get
 or
or
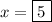 . The numerator is finite at these values
. The numerator is finite at these values
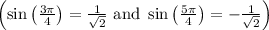 .
.
This means
 is not an asymptote. (C)
is not an asymptote. (C)