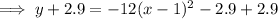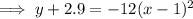Answer:
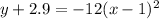
Explanation:
Vertex form of a quadratic function:

where:
- (h, k) is the vertex.
- a is some constant.
If a > 0, the parabola opens upwards.
If a < 0, the parabola opens downwards.
Given vertex: (1, -2.9)
Therefore:
Substitute the values of h and k into the formula:
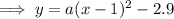
As the function has no x-intercepts, and the vertex is in Quadrant IV, the parabola will open downwards. Therefore, "a" will be negative. Without any further information, any number can be substituted for "a". Therefore, according to the given answer, let a = -12:
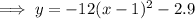
Note: If "a" was positive, the parabola would open upwards, which means there would be two x-intercepts (two points at which the curve intercepts the x-axis).
Finally, add 2.9 to both sides of the equation so that the equation is in the format of the given answer: