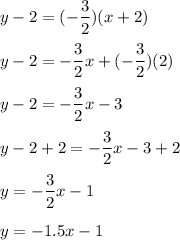Question

Find an equation for the perpendicular

bisector of the line segment whose
endpoints are (-8, -2) and (4, 6).

Answer 1

Answer: y=-1.5x-1

Explanation:

A(-8,-2) B(4,6) C(x,y) - the midpoint of the line

1. Calculate the coordinates of the midpoint of the segment using the formula:

`\displaystyle\\C(x,y)=((x_A+x_B)/(2) ,(y_A+y_B)/(2))\\\\ C(x,y)=((-8+4)/(2),(-2+6)/(2))\\\\ C(x,y)=((-4)/(2) ,(4)/(2))\\ C(x,y)=(-2,2)\\Thus,\ C(-2,2)`

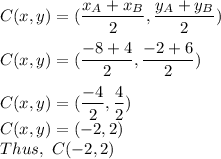
2. Find the slope of the line AB using the formula:

`\displaystyle\\The\ slope=(y_B-y_A)/(x_B-x_A) \\\\The\ slope=(6-(-2))/(4-(-8)) \\\\The\ slope=(6+2)/(4+8) \\\\The\ slope=(8)/(12) \\\\The\ slope=(2)/(3)`

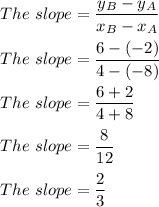
3. Find the slope of the line perpendicular to the line AB:

`\displaystyle\\The \ \perp slope=-(1)/(the\ slope) \\\\The \ \perp slope=-(1)/((2)/(3) ) \\\\The \ \perp slope=-(3)/(2)`

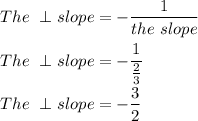
4. Find an equation for the perpendicular bisector of the line segment:

`\displaystyle\\The \perp\ slope=(y-y_C)/(x-x_C) \\\\-(3)/(2)=(y-2)/(x-(-2)) \\-(3)/(2) =(y-2)/(x+2) \\`

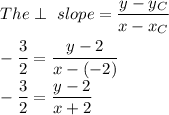
Multiply both parts of the equation by (x+2):

`\displaystyle\\y-2=(-(3)/(2) )(x+2)\\\\y-2=-(3)/(2)x+(-(3)/(2))(2)} \\\\y-2=-(3)/(2)x-3 \\\\y-2+2=-(3)/(2)x-3+2\\\\ y=-(3)/(2)x-1\\\\ y=-1.5x-1`