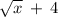Answer:
4th choice
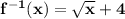
Explanation:
Definition of the inverse of a function
A function g is the inverse of a function f if whenever y=f(x) then x=g(y). In other words, applying f and then g is the same thing as doing nothing. We can write this in terms of the composition of f and g as g(f(x))=x. The domain of f becomes the range of g and the range of f becomes the domain of g
To solve for the inverse of the function
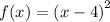
Let

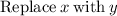
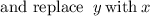

Switch sides
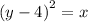
Take square roots on both sides
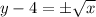
Add 4 on both sides to solve for y
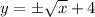
We have two solutions

To determine which one of these to be chosen not that in the given choices we can eliminate the first two since x cannot be negative
The third choice can also be eliminated since
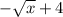 is a decreasing function for
is a decreasing function for
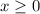
So the last answer choice is correct and the inverse of
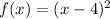
is given by

Answer:4th choice
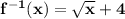
Note
Domain of (x-4)² is [4, ∞) since x ≥ 4 and (x-4)² cannot be negative
Range of (x-4)² is [0, ∞)
Domain of
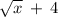 is [0, ∞)
is [0, ∞)
Range of
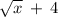 is [4, ∞)
is [4, ∞)
so indeed the domain of (x-4)² has become the range of
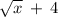 and the range of (x-4)² has become the domain of
and the range of (x-4)² has become the domain of