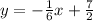Question

Write an equation in slope intercept form for the line perpendicular to y=6x+4 that passes through the point (-3,4)

Answer 1

Answer:
`y = -(1)/(6)x + (7)/(2)`

Explanation:

The slope of the line perpendicular is always the negative reciprocal of the line you're given.

So, in this case, the slope in y = 6x + 4, is 6 (the coefficient in front of the x). The negative of this is -6, and then do the reciprocal which is -1/6.

Next, we are given the the point that it passes through, which is (-3, 4). We have to use point slope formula for this which is given by:

`y - y_(1) = m(x-x_(1))`

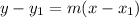
We know m = -1/6 from before, and
`x_(1) = -3`, and
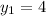`y_(1) = 4` (this comes from the given point). Plugging these in we have:

`y - 4 = -(1)/(6) (x - (-3))`

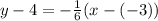
Point slope intercept form is given by
`y = mx + b` so to rearrange it to this form, we have to distribute the -1/6 and isolate y.

After distributing we get:

`y - 4 = -(1)/(6)x -(1)/(2)`

Then isolating the y term we get:

`y = -(1)/(6)x + (7)/(2)`

Answer 2

y=-1/6x+21

Explanation:

The slope of line y=6x+4 is 6

For two perpendicular lines,the gradient of one is the negative reciprocal of the other

Therefore the gradient of the other line=-1/6

Equation of that line

=>(y-y1)=m(x-x1)

y-4=-1/6(x--3)

y-4=-1/6(x+3)

6y-24=-x-3

6y=-x-3+24

6y=-x+21

y=-1/6x+21