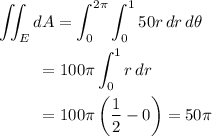Question

Find the surface area of that part of the plane 4x 5y z=74x 5y z=7 that lies inside the elliptic cylinder x225 y2100=1

Answer 1

Solve for
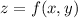`z=f(x,y)` in the plane equation.

`4x + 5y + z = 7 \implies f(x,y) = z = 7 - 4x - 5y`

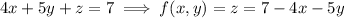
Let
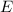`E` be the set of points in the plane
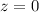`z=0` bounded by the ellipse
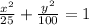`(x^2)/(25)+(y^2)/(100)=1`, i.e.

`E = \left\{(x,y) ~:~ (x^2)/(25) + (y^2)/(100) \le 1\right\}`

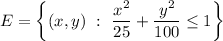
Then the area of the plane bounded by the elliptic cylinder is

`\displaystyle \iint_E dA = \iint_E \sqrt{1 + \left((\partial f)/(\partial x)\right)^2 + \left((\partial f)/(\partial y)\right)^2} \, dx \, dy \\\\ ~~~~~~~~ = \iint_E √(1 + (-4)^2 + (-5)^2) \, dx\, dy \\\\ ~~~~~~~~ = √(42) \iint_E dx \, dy`

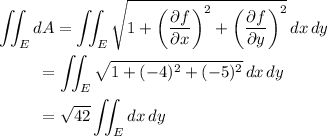
which is simply √42 times the area of the ellipse in the plane
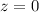`z=0`. This ellipse has a minor axis of length 5 and a major axis of length 10, so its area is π•5•10 = 50π, and so the area of the plane in question is 50√42 π.

To confirm this result: In polar coordinates, with

`\begin{cases}x(r,\theta) = 5r\cos(\theta) \\ y(r,\theta) = 10r\sin(\theta) \\ (x^2)/(25)+(y^2)/(100)=r^2\end{cases}`

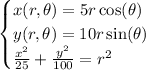
the area element is

`dA = \begin{vmatrix}(\partial x)/(\partial r)&(\partial x)/(\partial\theta) \\ (\partial y)/(\partial r) & (\partial x)/(\partial\theta)\end{vmatrix} \, dr \, d\theta \\\\ ~~~~~~~~ = \begin{vmatrix}5\cos(\theta)&-5r\sin(\theta)\\10\sin(\theta)&10r\cos(\theta)\end{vmatrix} \, dr \, d\theta \\\\ ~~~~~~~~ = \left(50r\cos^2(\theta)+50r\sin^2(\theta)\right)\,dr\,d\theta \\\\ ~~~~~~~~ = 50r \, dr \, d\theta`

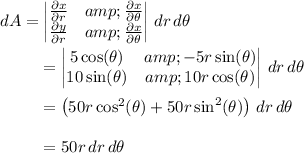
The ellipse can be parameterized by

`E = \left\{(r,\theta) ~:~ 0\le\theta\le2\pi \text{ and } 0\le r\le1\right\}`

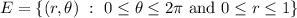
so that the integral for the area of the ellipse in the plane
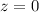`z=0` is

`\displaystyle \iint_E dA = \int_0^(2\pi) \int_0^1 50r \, dr \, d\theta \\\\ ~~~~~~~~ = 100\pi \int_0^1 r \, dr \\\\ ~~~~~~~~ = 100\pi\left(\frac12-0\right) = 50\pi`