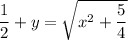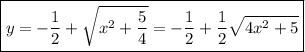Question

Solve the initial value problem.


`y' = (2x)/(1 + 2y) , \\ y(1) = 1`





​

Answer 1

Separate the variables:

`y' = (dy)/(dx) = (2x)/(1+2y) \implies (1+2y) \, dy = 2x \, dx`

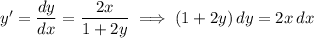
Integrate both sides:

`\displaystyle \int(1+2y) \, dy = \int 2x \, dx[/tex\</p><p>[tex]y + y^2 = x^2 + C`

Use the given initial condition to solve for C :

`1 + 1^2 = 1^2 + C \implies C = 1`

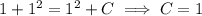
So the particular solution is

`\boxed{y + y^2 = x^2 + 1}`

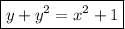
which you can also solve explicitly for y as a function of x. By completing the square on the left side, we have

`y + y^2 = x^2 + 1`

`\frac14 + y + y^2 = x^2 + \frac54`

`\left(\frac12 + y\right)^2 = x^2 + \frac54`

`\frac12 + y = \pm √(x^2+\frac54)`

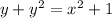
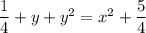
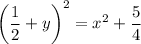
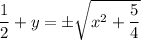
Note that y(1) = 1 is positive, so the right side should involve the positive square root:

`\frac12 + y = √(x^2+\frac54)`

`\boxed{y = -\frac12 + √(x^2+\frac54) = -\frac12 + \frac12 √(4x^2+5)}`