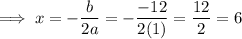Answer:
x = 6
Step-by-step explanation:
The axis of symmetry of a parabola is the x-value of its vertex.
For a quadratic function in the form
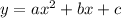 , the x-value of the vertex is:
, the x-value of the vertex is:
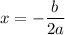
Given function:
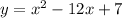
Therefore:
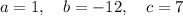
So the axis of symmetry of the given quadratic function is: