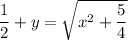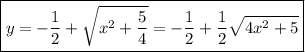Solve the initial value problem. y' = (2x)/(1 + 2y) , \\ y(1) = 1

Question

asked Jan 14, 2023 11.6k views

1 Answer

Benjamin Bihler · Answer 1 · 2023-01-19T18:06:46+0000

Separate the variables:

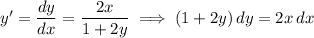
$y' = (dy)/(dx) = (2x)/(1+2y) \implies (1+2y) \, dy = 2x \, dx$

Integrate both sides:

$\displaystyle \int(1+2y) \, dy = \int 2x \, dx[/tex\</p><p>[tex]y + y^2 = x^2 + C$

Use the given initial condition to solve for C :

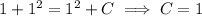
$1 + 1^2 = 1^2 + C \implies C = 1$

So the particular solution is

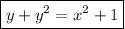
$\boxed{y + y^2 = x^2 + 1}$

which you can also solve explicitly for y as a function of x. By completing the square on the left side, we have

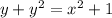
y + y^2 = x^2 + 1

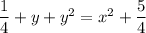
$\frac14 + y + y^2 = x^2 + \frac54$

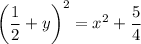
$\left(\frac12 + y\right)^2 = x^2 + \frac54$

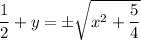
$\frac12 + y = \pm √(x^2+\frac54)$

Note that y(1) = 1 is positive, so the right side should involve the positive square root:

$\frac12 + y = √(x^2+\frac54)$

$\boxed{y = -\frac12 + √(x^2+\frac54) = -\frac12 + \frac12 √(4x^2+5)}$