Solve the initial value problem. y' =(3 + y)(1 - y) , \\ y(0) = 1 ​

Question

Solve the initial value problem.

`y' =(3 + y)(1 - y) , \\ y(0) = 1`
​

Answer 1

Answer: I have providedAnswer work on two separate pages.

Explanation:

Answer 2

Separate the variables:

`y' = (dy)/(dx) = (3+y)(1-y) \implies (dy)/((3+y)(1-y)) = dx`

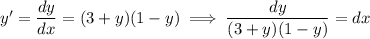
On the left, take the partial fraction decomposition:

`(1)/((3+y)(1-y)) = \frac a{3+y} + \frac b{1-y}`

`(1)/((3+y)(1-y)) = (a(1-y) + b(3+y))/((3+y)(1-y))`

`(1)/((3+y)(1-y)) = ((b-a)y+a-3b)/((3+y)(1-y))`

`\implies (b-a)y +a-3b = 1`

`\implies \begin{cases}b-a=0\\a-3b=1\end{cases} \implies a=b=-\frac12`

`\implies \frac1{(3+y)(1-y)} = -\frac12 \left(\frac1{3+y} + \frac1{1-y}\right)`

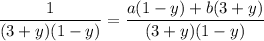
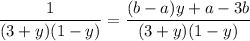
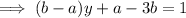
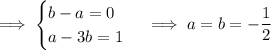
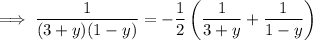
Now integrate both sides:

`\displaystyle \int -\frac12 \left(\frac1{3+y} + \frac1{1-y}\right) \, dy = \int dx`

`-\frac12 \left(\ln|3+y| + \ln|1-y|\right) = x + C`

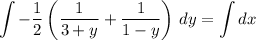
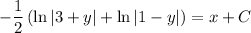
Normally, at this point you would solve for C using the initial condition. However, in this case we have y(0) = 1, and ln|1 - 1| = \ln(0) is undefined.

Notice that if we let y be a constant function, then y' = 0.

Knowing that y(0) must be equal to 1, let's take our solution to be y(x) = 1. Then y'(x) = 0, and on the right side we have 1 - y = 1 - 1 = 0 as well.

So, the solution to this equation is y(x) = 1.